Влияние частоты вращения рабочего колеса насоса на его характеристики

Заданные характеристики насоса, полученные при частоте вращения N, можно пересчитать, используя формулы (1.16) — (1.18), и построить ряд других характеристик для различных частот вращения.

На рис. 1.21 показано построение новых характеристик при п₂ по заданным характеристикам. Если на напорной характеристике (Q—взять произвольную точку (например, 1) с параметрами Qi и Hi, то на основании уравнений (1.16) и (1.17) подача и напор при частоте вращения п_2:

Откладывая значения Q₂ и Н₂, находим точку, принадлежащую характеристике при частоте вращения п₂. Производя подобные вычисления и построения для других точек и соединяя их плавной кривой, получим новую напорную характеристику (Q—Н)_п2 при частоте вращения п₂.

На основании формул (1.16), (1.17) можно записать:

откуда

Из последнего уравнения следует, что переходная кривая при пересчете параметров Q и И на другую частоту вращения является квадратичной параболой с вершиной в начале координат. Эта парабола называется кривой пропорциональности при различных частотах вращения, она же одновременно является кривой одинаковых значений КПД.

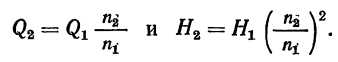
Таким образом, при непрерывном изменении частоты вращения от п_{ до п₂ значения Q и Н будут изменяться по закону параболы, т. е. напорная характеристика будет перемещаться (приблизительно) параллельно самой себе (при увеличении частоты вращения — вверх, а при уменьшении — вниз). Характеристика Q—т) будет перемещаться при уменьшении частоты вращения влево, а при увеличении — вправо.

Аналогично пересчитывают и характеристику Q—N, используя уравнения (1.16), (1.18). Кривая пропорциональности при этом будет представлять Кубическую параболу.

Рассмотренные выше построения выполняют в эксплуатационных расчетах при регулировании подачи насоса изменением частоты вращения рабочего колеса.