Интегрально-кинетический метод
Интегрально-кинетический метод (ИКМ) также основан на решении интегрального уравнения молекулярного переноса. Его название связано с тем, что в качестве исходной применена интегральная форма записи кинетического уравнения, которое категорией функции распределения f (г, v, г) исчерпывающим образом описывает поведение газа.
Пользуясь соотношениями динамики разреженных газов, для произвольной точки г в вакуумируемом пространстве можно записать:
Числитель в (4.25) дает поток молекул, не поглотившихся в полости насоса и вылетевших обратно в камеру, а знаменатель — поток молекул, падающих на вход насоса;
коэффициент обратного рассеяния для закрытой структуры:


[индекс пад при символе V в формулах (4.24) — (4.26) опущен].
Решая систему (4.20), можно построить также поле молекулярных концентраций, найти индикатрисы плотности выходящих и рассеиваемых потоков, вычислить коэффициент возврата и т. п.
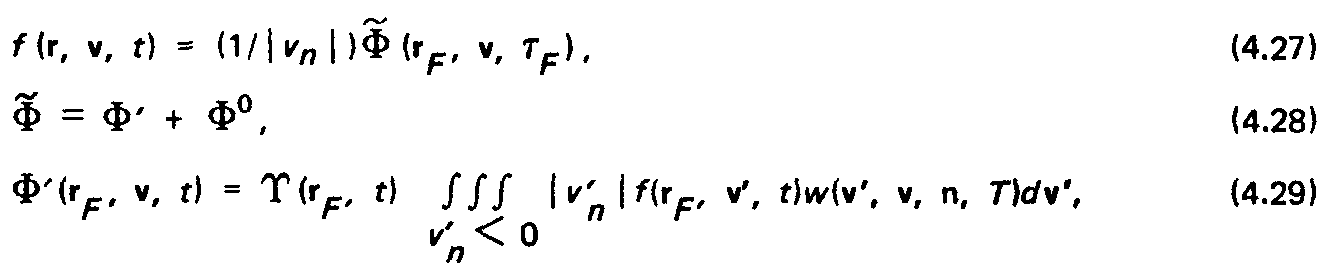

Поскольку векторы v и v взаимно независимы, соотношение (4.29) можно представить в виде:
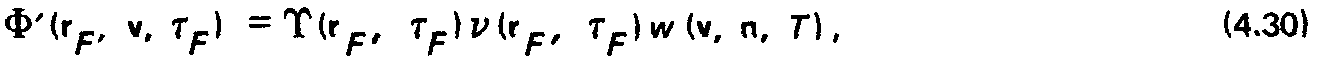

Подстановка (4.27), (4.28) и (4.30) в соотношение (4.31) дает интегральное уравнение для плотности потока молекул на площадку вокруг точки г р :
Интегральное уравнение (4.32) является исходным для получения молекулярных характеристик. Полагая, что анализируемая структура состоит из т поверхностей, область интегрирования в (4.32) можно представить состоящей из т частей:
Зональным методом систему (4.34) можно преобразовать к системе линейных алгебраических уравнений. Разбив F. на к. зон, получим
Коэффициенты, определяемые геометрией структуры и моделью взаимодействия молекул с поверхностями, представлены в табл. 4.2:
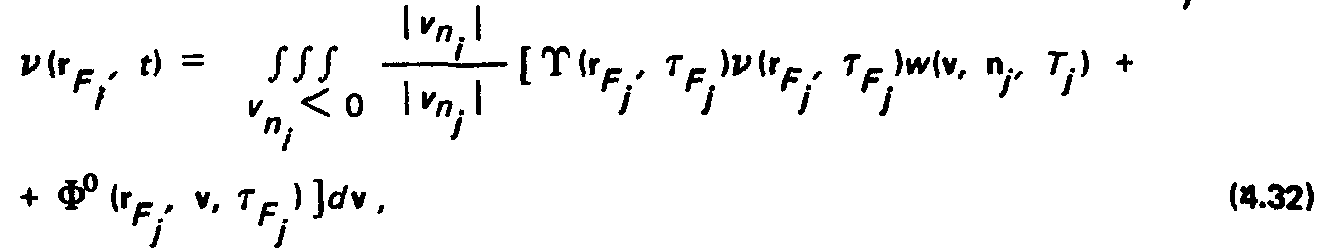



где:
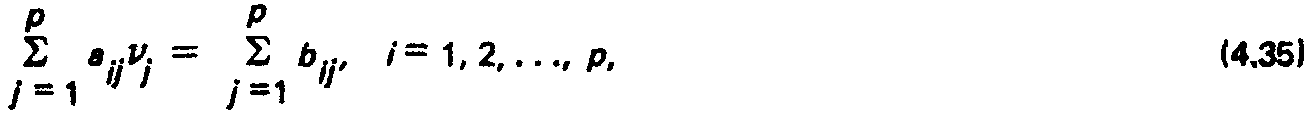

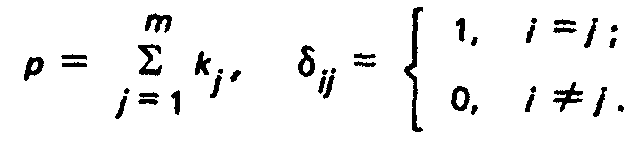

Свободный член by определяется параметрами собственного источника молекул, находящегося в данной зоне поверхности F.. Для источника с косинусным распределением эмиттируемого потока при изотропном распределении где интегрирование ведется по всем возможным направлениям скорости. Характеристическая функция в соответствии с (4.30) определена здесь через плотности потока V, которые, в свою очередь, находятся из системы (4.35).
Плотность потока молекул в заданном направлении в окрестности точки Гр, выбранной на произвольной поверхности F: где F* — поверхность канала, эмигрирующая молекулы в рассматриваемом направлении. Интегральные характеристики Р, Г и Ео „ определяются по формулам (4.24) — (4.26).
Сопоставим МУК и интегрально-кинетический метод (ИКМ). Коэффициенты а., системы (4.35) представляют собой вероятность прямого молекулярного обмена между элементарной площадкой и поверхностью конечных размеров, учитывающую не только их взаимную ориентацию, но и параметры взаимодействия молекула—поверхность. При диффузном рассеянии молекул стенкой в соответствии с (4.15) и (4.36) можно записать:
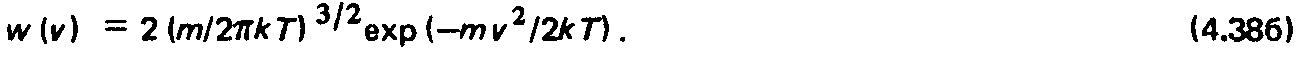

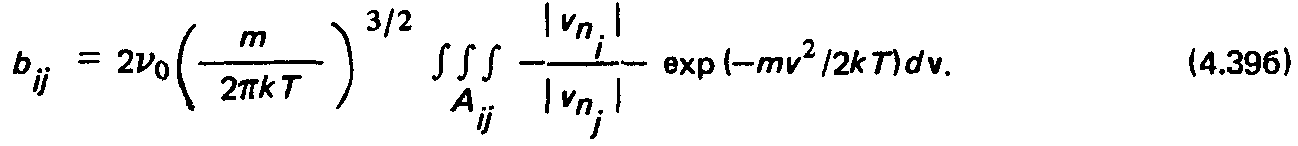
Формулы (4.38) и (4.39) справедливы в предположении, что скорость молекул определяется температурой поверхности; Vq — плотность эмиттируемого потока частиц. При отсутствии источника Ф = 0; b.j = 0.
Искомые характеристики можно теперь легко рассчитать решением системы (4.35) и некоторыми дополнительными вычислениями. В частности, молекулярная концентрация вокруг точки:

Индикатриса плотности потока в выходном сечении канала (рис. 4.4), вводимая соотношением:
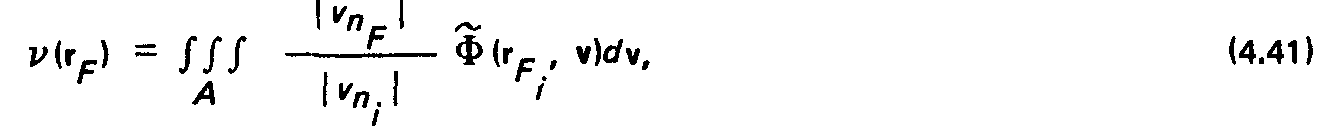

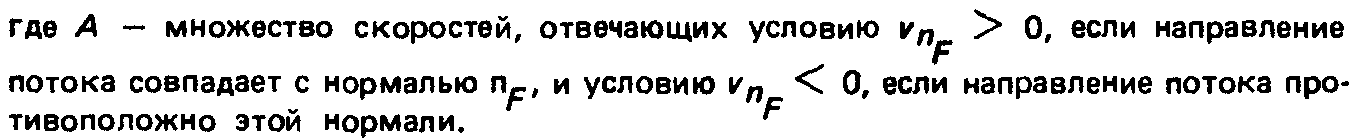

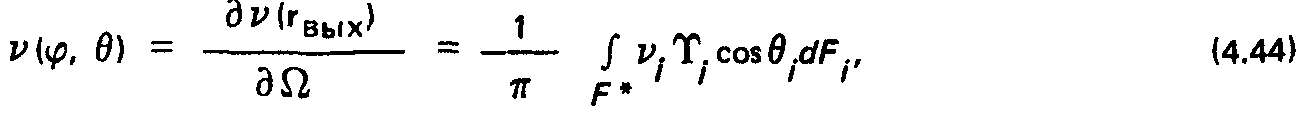
Чисто вычислительная процедура определения a.j существенно проще, чем нахождение УК. Отсюда вытекает вывод, касающийся целесообразных областей применения каждого из методов. МУК предпочтителен для расчета сравнительно простых структур. В частности, если геометрические УК известны, то решение практических задач с помощью МУК занимает сравнительно мало времени и может быть выполнено даже без ЭВМ. И КМ более целесообразен при анализе структур повышенной сложности, в которых расчет УК затруднителен.
При усложнении геометрической структуры громоздкость вычислительных операций быстро возрастает. Эту трудность можно обойти созданием универсальной логико-математической модели молекулярного переноса, излагаемой в следующем параграфе.
Основу метода эквивалентных поверхностей (МЭП) составляет последовательное замещение реальных элементов ВС их простыми газокинетическими эквивалентами. Этим эквивалентам приписывают газокинетические характеристики, определяемые из условия тождественности молекулярных характеристик в реальной структуре и в ее математической модели. Например, за эквивалентную поверхность для насоса принимают плоскость его подсоединения к камере. Ей приписывают те свойства взаимодействия” с потоками молекул, которыми обладает замещаемый насос. По отношению к камере эта плоскость наделяется свойством поглощать” падающие молекулы с вероятностью, равной коэффициенту захвата насоса, а по отношению к насосу — полностью поглощать падающие на нее молекулы. Ей приписывают также свойство эмиттировать потоки молекул двоякого рода. По отношению к камере потоки, эмиттируемые плоскостью, тождественны потокам, истекающим из насоса, если для него Г 1. По отношению же к насосу плоскость эмиттирует поток, тождественный падающему на него из камеры.
Таким образом, эквивалентная поверхность представляет собой пограничную между двумя областями условную поверхность, которой в зависимости от того, частью какой из областей ее рассматривают, приписывают различные характеристические функции. Благодаря такому подходу на первом этапе вычисления рассматривают простую расчетную модель, содержащую главные компоненты анализируемой структуры и некоторое число эквивалентных поверхностей. Определяют распределение молекулярных характеристик в этой модели и сравнивают их с теми, которые были приняты при формировании первичных характеристик эквивалентных поверхностей. Если обнаруживается существенное расхождение, то на следующем этапе анализируют потоки в замещенных элементах и переходят ко второму шагу итераций и т. д.
Из сказанного ясно, что в МЭП не существен способ вычисления самих молекулярных характеристик. Для определенности в дальнейшем сформулированная Концепция изложена с позиций ИКМ.
Рассмотрим произвольную структуру, выделив в ней области.

