Структурно-периодические вакуумные системы

В-третьих, как особенно наглядно видно из индикатрис для составных трубопроводов, с помощью последних возможно формирование направленных молекулярных пучков с малой угловой расходимостью. Это свойство составных трубопроводов можно эффективно использовать при структурно-геометрической оптимизации ВС.

При вычислении проводимости геометрически более сложных каналов применим метод Монте-Карло (см. гл. 4). Однако его практическое использование проблематично ввиду ограничений вычислительного характера. В этих случаях удобна упрощенная методика, которая позволяет обойти указанные ограничения.

Рассматриваемую систему трубопровод — камеры можно представить как предельное состояние гипотетической системы, в которой между элементарными каналами размещены промежуточные камеры большого объема. Наличие промежуточных камер позволяет удовлетворить сформулированному выше требованию равновесности состояния газа на входе в каждый канал. Поэтому, следуя принципу аддитивности сопротивлений каналов Z. при их последовательном соединении, проводимость гипотетического трубопровода между двумя камерами можно представить

Переход от гипотетической системы к реальному трубопроводу приводит к деформации пространственного распределения молекулярного потока на входе второго и последующих каналов, что нарушает условие равновесности и делает некорректным применение формулы (3.3) для вычисления проводимости всех каналов, кроме первого. Поскольку полное сопротивление каждого канала складывается из сопротивлений входного отверстия, участка трубопровода между входным и выходным сечениями и выходной диафрагмы, такой переход логично истолковать как уменьшение полного сопротивления на сопротивление входного сечения Z_o/. Сопротивление первого канала при указанном переходе не меняется.

Тогда сопротивление каждого из каналов, кроме первого, после их непосредственного сопряжения полное сопротивление трубопровода его проводимость где n — число элементов периодичности.

Как показывает детальный анализ, точность изложенной методики вполне приемлема для инженерной практики. На ее основе с учетом (3.6) и (3.7) получены приведенные ниже формулы для вычисления вакуумных характеристик структурно-периодических систем ЭФУ.

Диафрагмированный волновод линейных ускорителей электронов с бегущей волной (рис. 3.8, табл. 3.3):

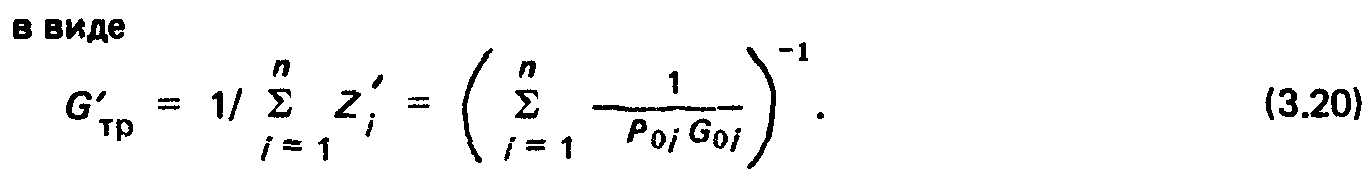
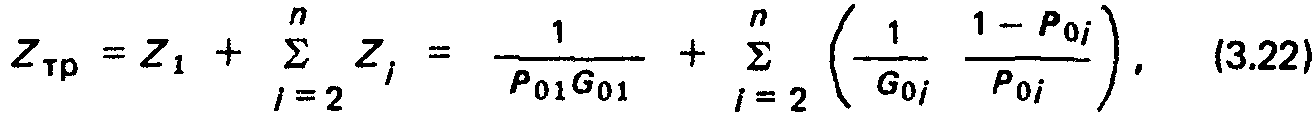
В частности, для однородных структурно-периодических трубопроводов:

Перепад давлений между торцевыми сечениями волновода где s — число отверстий диаметром д₀ каждое, соединяющих внутреннюю полость волновода с кожухом; q_K и q — удельная скорость десорбции с поверхности кожуха и наружной поверхности волновода соответственно; D — внутренний диаметр кожуха; Роотв ^— коэффициент Клаузинга для этих отверстий.

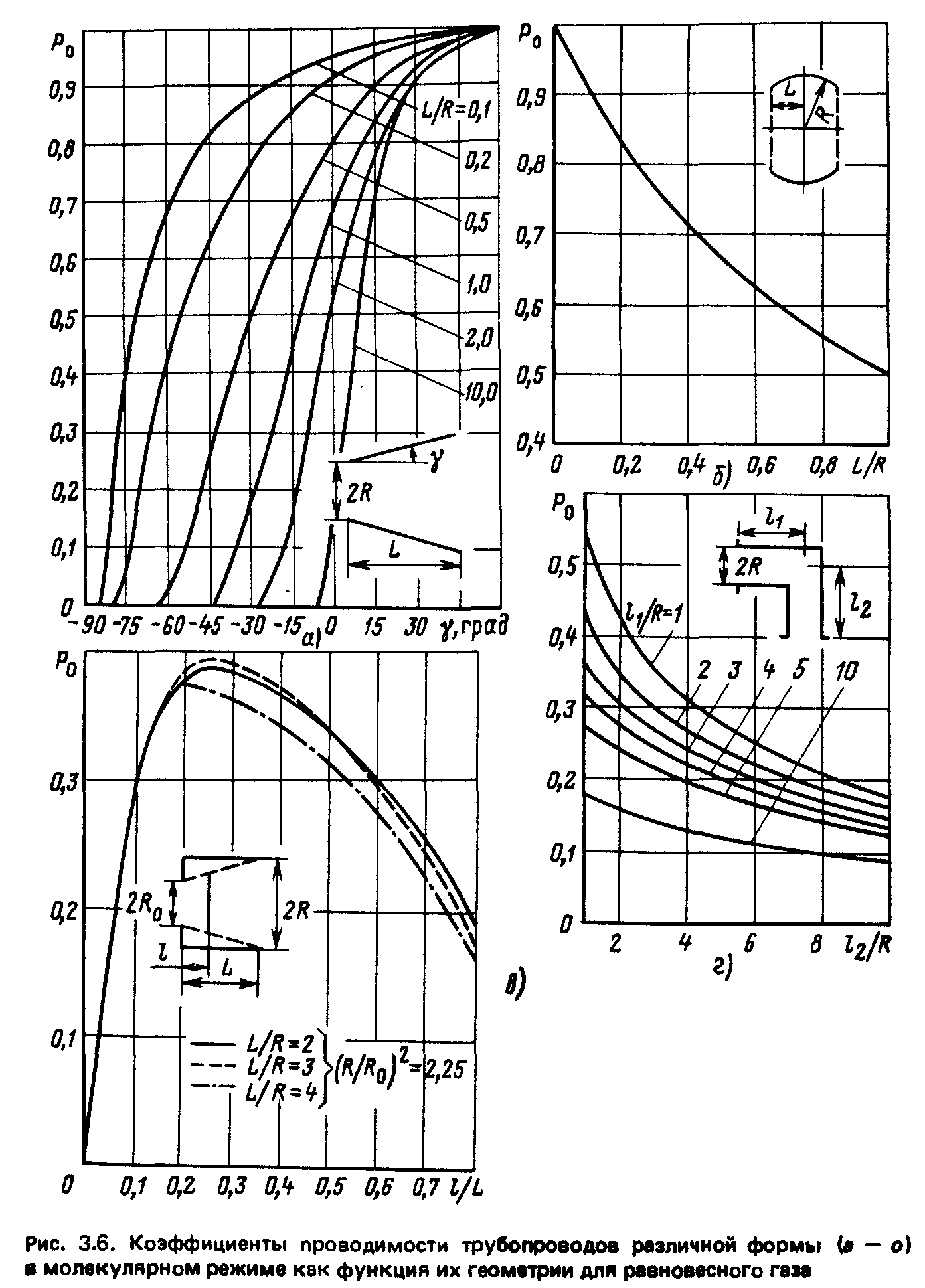
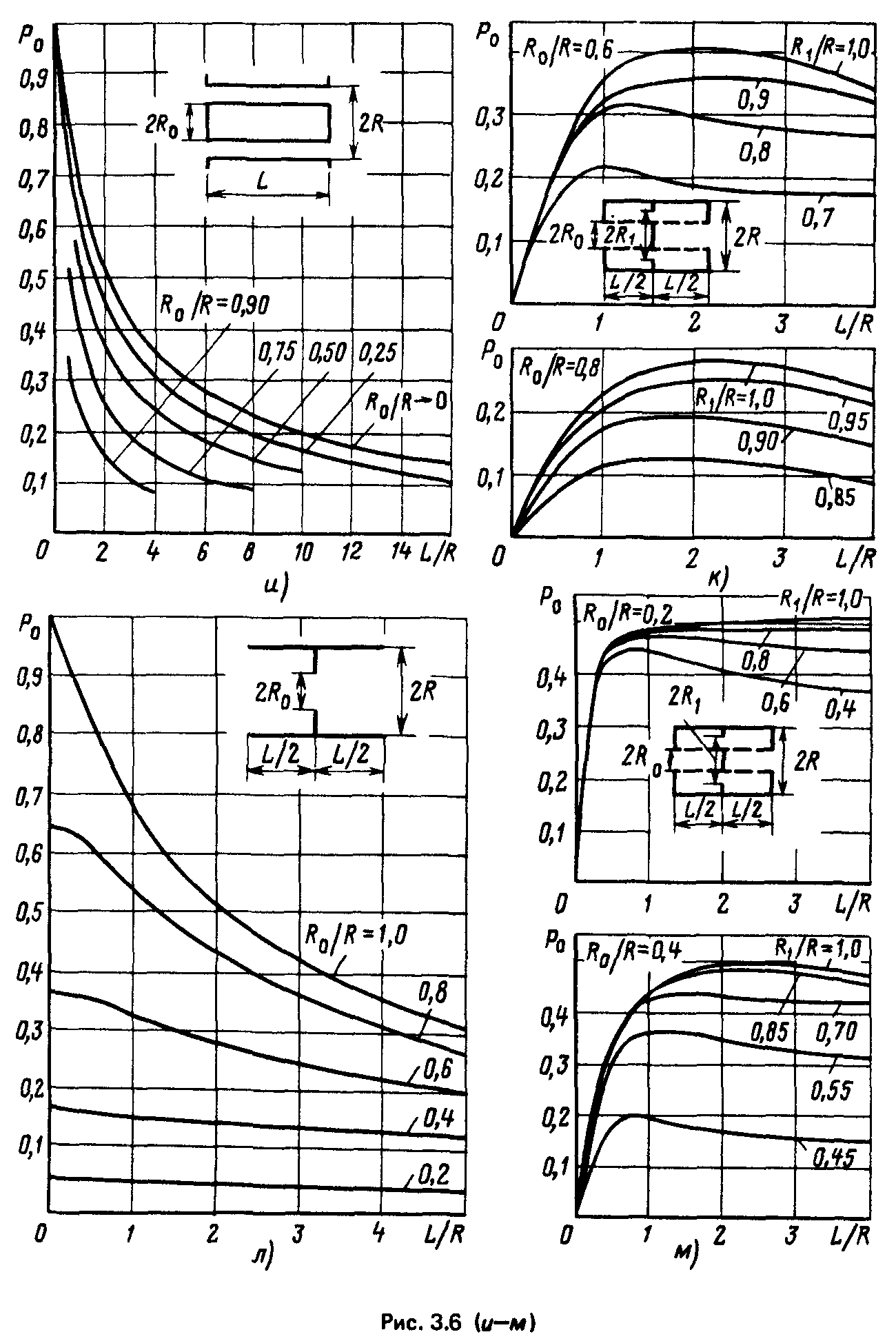
Ускорительная трубка высоковольтных ускорителей, содержащая в каждом электроде центральное отверстие диаметром d₀ и периферийных отверстий диаметром 2г каждое. Проводимость участка трубки длиной х где t — расстояние между соседними электродами; Р_о — коэффициент проводимости расчетной ячейки, определяемый по рис. 3.6, д в зависимости от отношений t/d_T и d_3KBldj; d₁ — внутренний диаметр диэлектрических колец.

Перепад давлений между торцевыми сечениями трубки, определяемый десорбционной нагрузкой с поверхности колец и электродов:

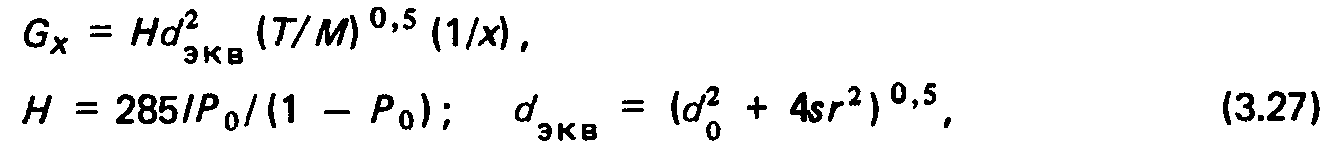
Перепад давлений между торцевыми сечениями волновода, размещенного в вакуумном кожухе:

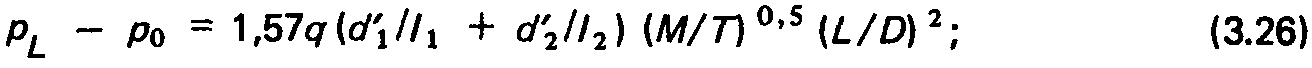
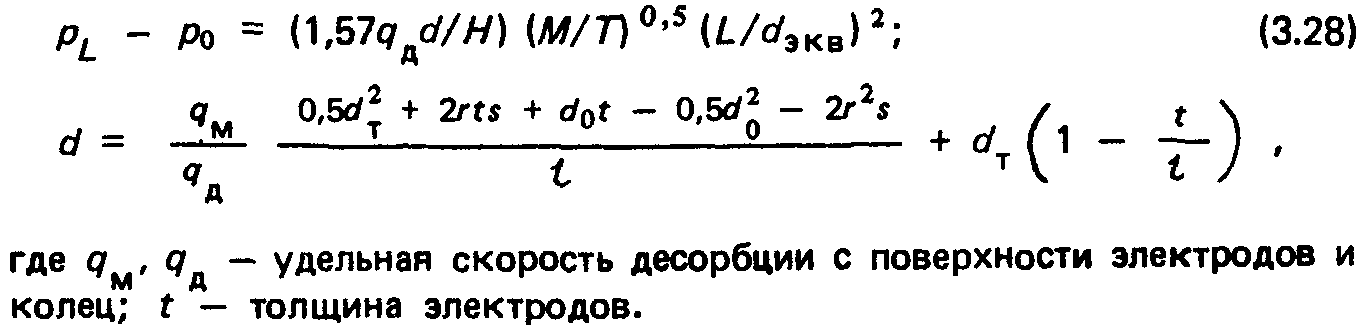
Приведенные формулы позволяют определить потери пучка из-за взаимодействия с остаточным газом. В частности, функции сохранения пучка при рассеянии и при перезарядке [сечение перезарядки а (к) аппроксимируется степенной зависимостью вида о (к) = а₀Е~^а к -x/L}:

Учитывая, что рон обычно существенно меньше остальных слагаемых, взаимосвязь между основными характеристиками ВС можно выразить в форме:

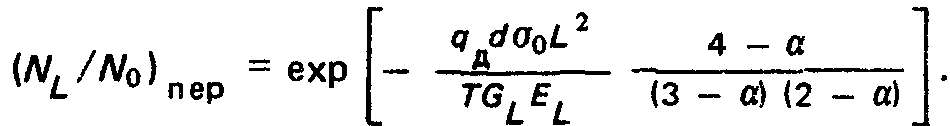
Коллекторная система откачки малоапертурных камер. Рассматривая в силу симметрии один участок длиной L = tn, содержащий насосы, секции коллектора и камеры и соединительные вакуумпроводы, полагая число соединительных вакуумпроводов п = (2Аг + 1)Л/, где /V- число равномерно распределенных насосов с одинаковыми параметрами ро_н, So_H, можно записать:

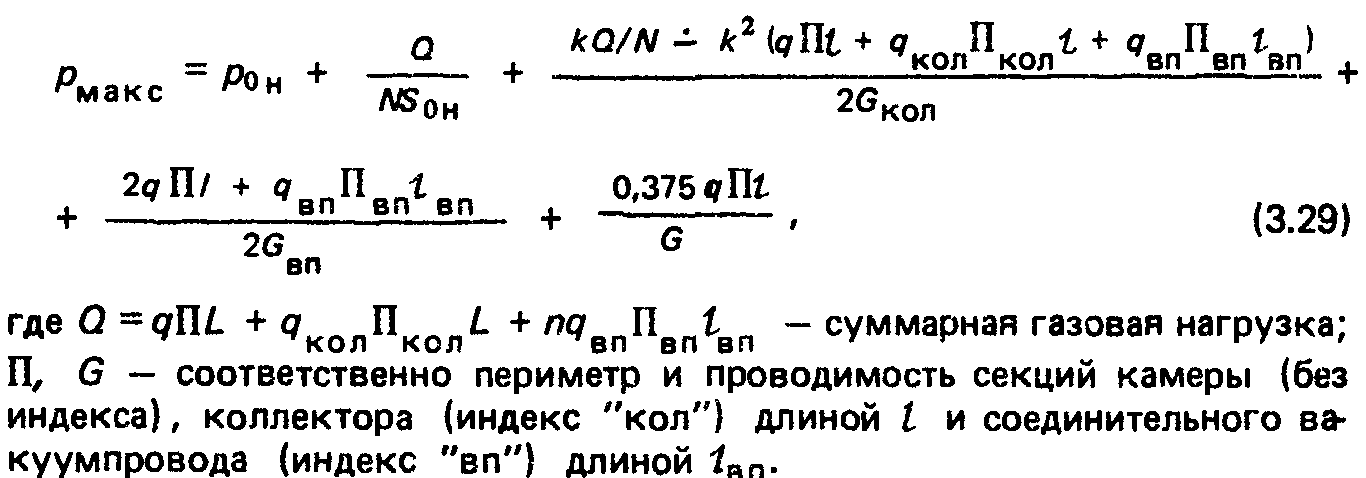
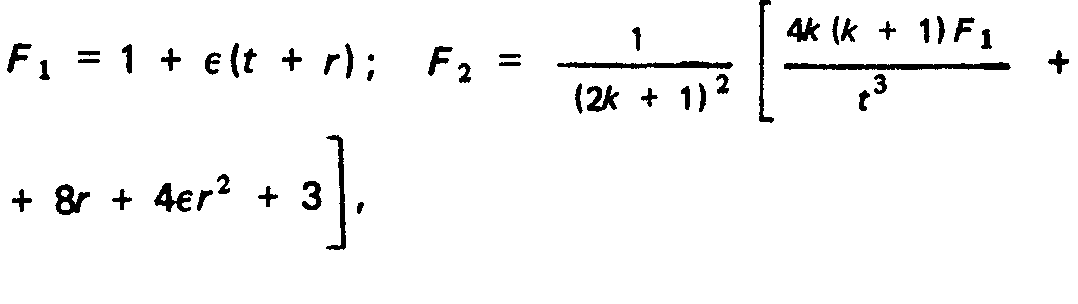
Задаваясь допустимым давлением Р_доп, соотношение (3.30) можно переписать в виде:

Систему (3.36) можно преобразовать в два независимых неоднородных уравнения вида:

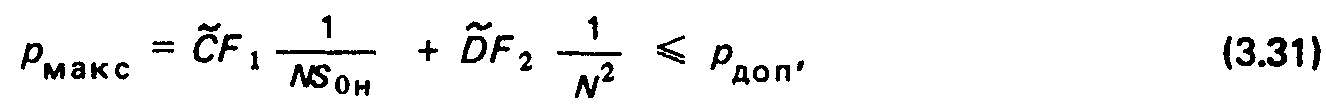
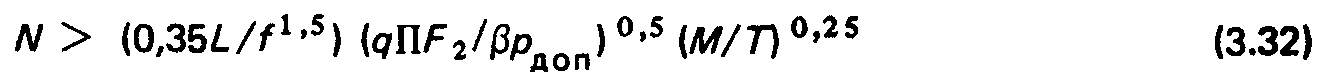
Рассмотрение ВС с дискретно меняющимся профилем завершим анализом системы ионный источник — вакуумная камера при импульсном напуске газа. Анализируемая система представляет собой две камеры, откачиваемые насосами с параметрами р_Он1, Рон2 ^и 5онь онг ^и соединенные диафрагмой проводимостью G; поток рабочего газа О(Г) поступает в первую камеру. В предположении, что сорбция газа стенками описывается линейной частью уравнения Ленгмюра, уравнения газового баланса в каждой из камео можно записать в виде.

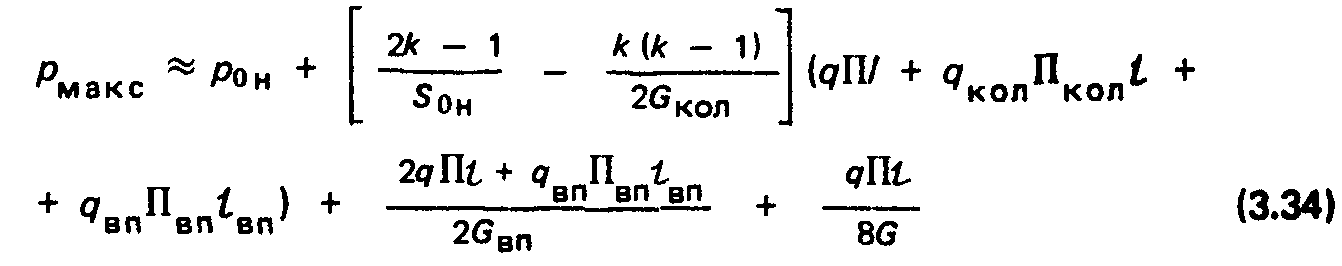
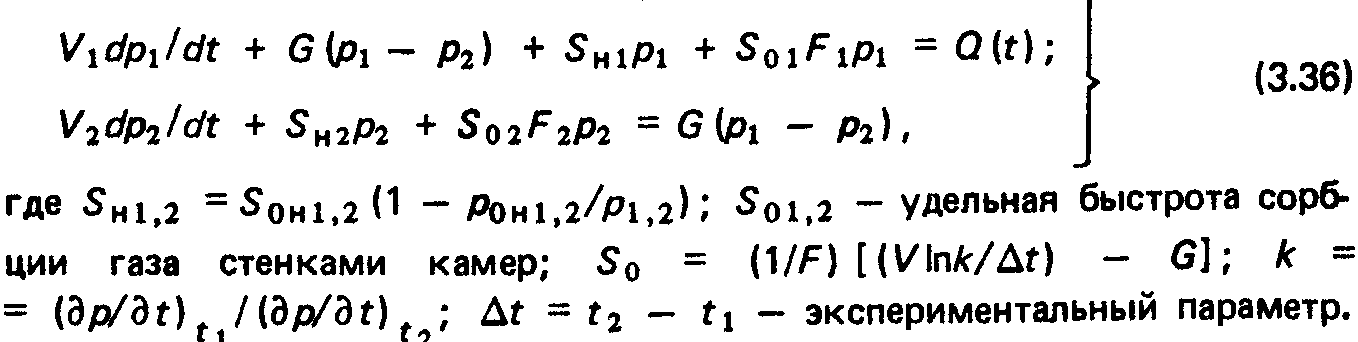
Формулы (3.37) и (3.38) позволяют, задавшись функцией Q(t), определить давление в каждой из камер.

В нелинейных системах качественный характер взаимодействия пучка заряженных частиц и плазмы с вакуумной средой зависит от интенсивности, энергии или других характеристик пучка (плазмы). В этом случае воздействие вакуумной среды на пучок или плазму зависит от их параметров; столь же существенно, в свою очередь, влияют эти параметры на пространственно-временное распределение молекулярной концентрации, топографию, плотность и парциальный состав молекулярных потоков и другие газокинетические характеристики. В табл. 3.4 перечислены возможные физические механизмы, приводящие к нелинейности ВС, и типичные ЭФУ, где могут реализоваться эти механизмы.