Подобие насосов и формулы пересчета основных параметров
Геометрическое подобие заключается в пропорциональности изменения всех линейных размеров при сохранении равенства угловых размеров. При этом должен быть постоянным линейный коэффициент подобия:
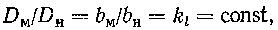

Кинематическое подобие применительно к гидравлическим машинам означает подобие параллелограммов скоростей я сходственных точках проточной части двух геометрически подобных машин при одинаковых режимах их работы.
Рассмотрим два геометрически подобных рабочих колеса: одно из них модельное (рис. 1.12, а), другое — натурное (рис. 1.12, б). При сходственных режимах работы параллелограммы скоростей выхода будут подобными. Таким образом, кинематическое подобие насосов можно выразить следующей зависимостью:
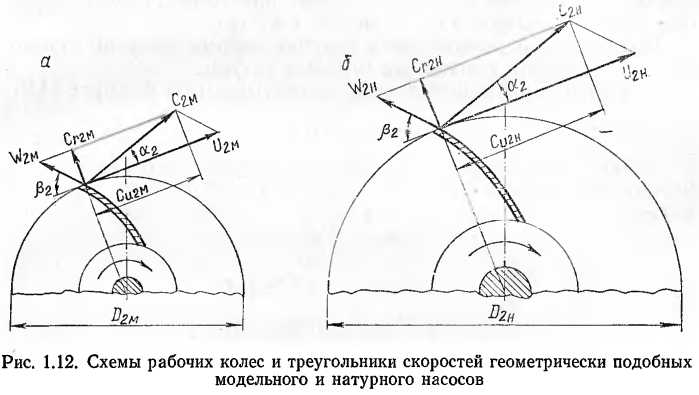
Геометрическое подобие также означает постоянство отношений любых сходственных линейных размеров:

Динамическое подобие предполагает пропорциональность сил, действующих в сходственных точках проточной части,, при сохранении геометрического и кинематического подобия. Динамическое подобие означает равенство критериев подобия, которыми являются числа Эйлера, Рейнольдса, Фруда и Струхаля:
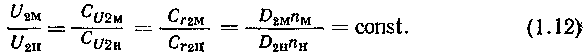

Последнее выражение имеет важное значение при моделировании насосов, так как оно устанавливает зависимость между энергетическими параметрами Q и Н модели и натуры.
На основании зависимостей подобия насосов получим соотношения технических параметров модели и натуры.
Подачу центробежного насоса подсчитывают по формулё (1.9).
Напор подобных насосов прямо пропорционален произведению диаметра колеса на выходе и частоты вращения во второй степени и гидравлическому КПД в первой степени.
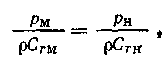

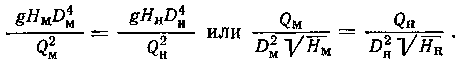
Характерным линейным размером насосов является D2 — внешний диаметр рабочего колеса.
Поэтому на основании уравнений (1.12) и (1.9)
Подача подобных насосов прямо пропорциональна частоте вр лцения, объемному КПД, коэффициенту стеснения в первой «степени и диаметру колеса на выходе в третьей степени.
Напор насоса определяют по формуле (1.7):

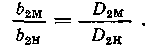

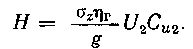

Для модели и натуры Оах=хя, поэтому, используя равенство (1.12), можно получить следующую зависимость:
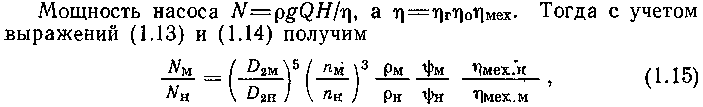
Мощность подобных насосов прямо пропорциональна диаметру колеса на выходе в пятой степени, частоте вращения в третьей степени, плотности жидкой среды, коэффициенту стеснения в первой степени и обратно пропорциональна механическому КПД в первой степени.
При проектировании насосов новых типов необходимо определять по заданным значениям Q, И и принятому п наиболее рациональные уже исследованные формы рабочих колес насосов. Сравнение колес различных типов производят по коэффициенту быстроходности (ng).

