Линейные вакуумные системы с распределенными параметрами

Рассмотрим элементарный участок dx протяженной камеры длиной L, периметром П (х), площадью поперечного сечения F (х) с распределенной газовой нагрузкой q(x}, не зависящей от р(х). Камера откачивается насосом, установленным в сечении х = 0. Баланс газа в элементарном объеме dV =F (x)dx определяется системой уравнений:

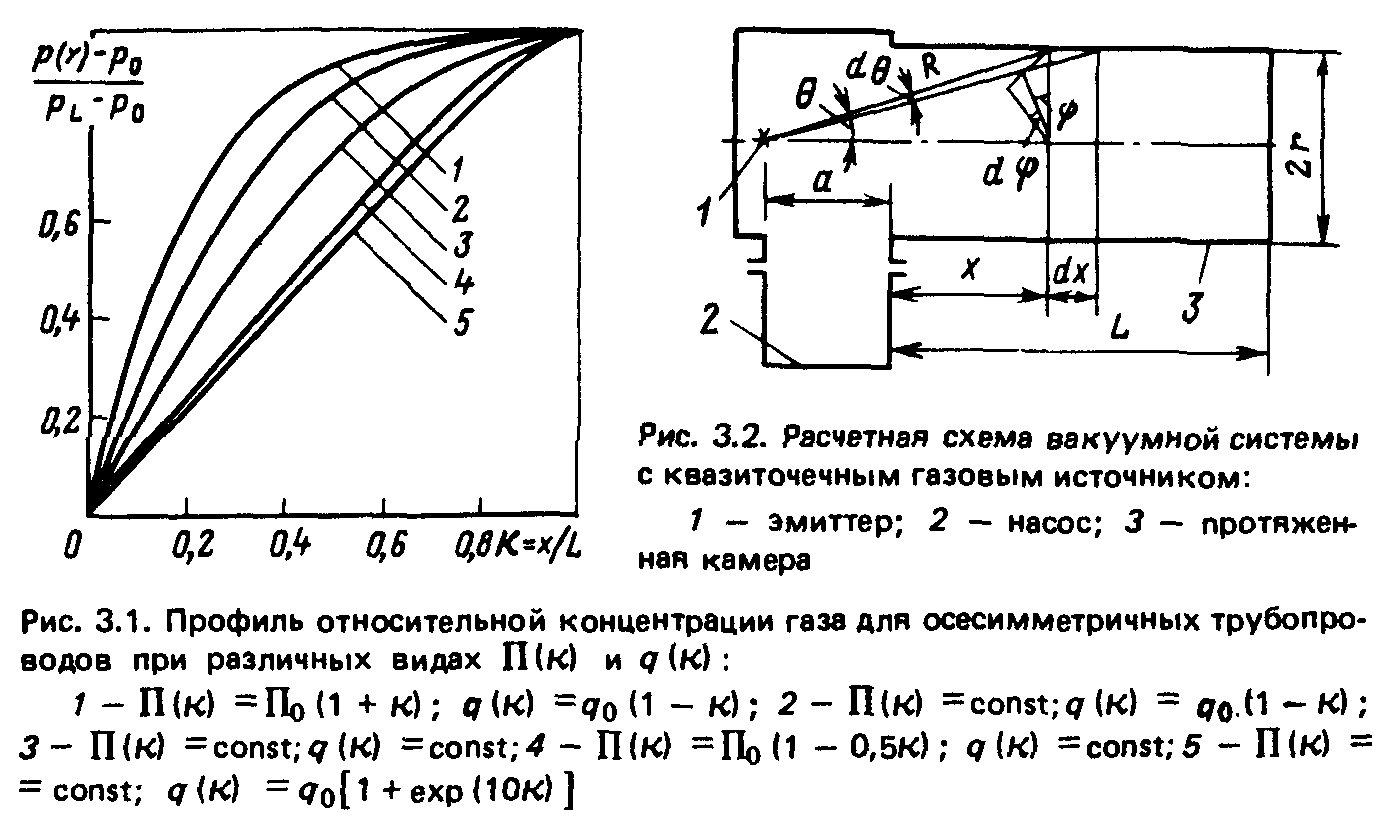
Формулы (3.6) и (3.7) являются базовыми при расчете вакуумных систем ионно- и электронопроводов, участков дрейфа пучков и линейных ВС других ЭФУ. С учетом широкой распространенности ЭФУ, в которых q (х) = var и П (х) = var (сканирующие и выводные устройства ускорителей прикладного назначения, технологические устройства электрофизического аппаратостроения, переходные патрубки термоядерных и ускорительных установок, системы дифференциальной откачки и т. п.), приведем значения [р(х) — p_Q]/(p_L — Ро) для наиболее распространенных видов функций q (к) и П (к), к = x/L, вычисленные по этим формулам (табл. 3.2 и рис. 3.1). Хорошо видны возможности управления профилем концентрации остаточного газа путем подбора параметров а (геометрия трубопровода), Р и у (состояние поверхности, температура трубопровода).

Рассмотрим еще одну распространенную линейную ВС с распределенными параметрами — систему с квазиточечным газовым источником. К таким системам относятся, например, плазменные и ионные инжекторы. Поток нейтральных частиц (газа) всегда сопутствует эмиттируемым источниками пучкам ионов или плазменных сгустков. Истекающие из эмиссионного отверстия молекулярные пучки в результате рассеяния.

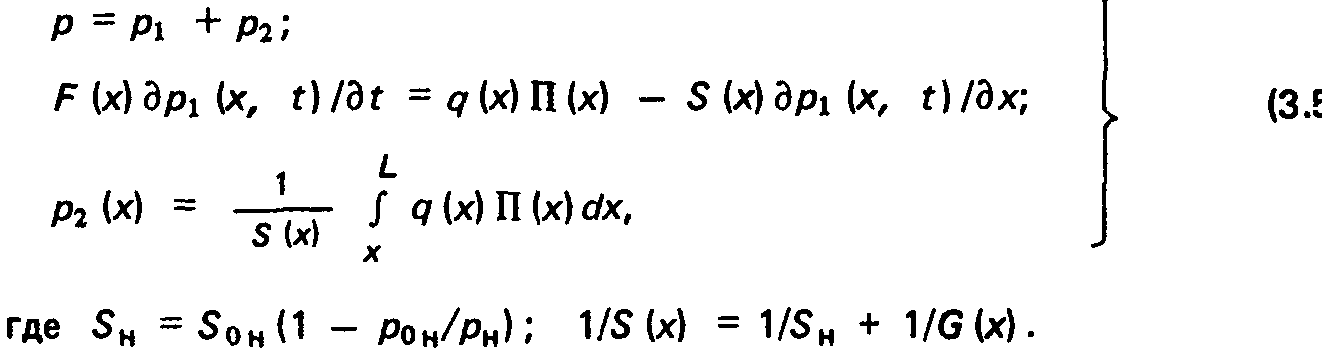
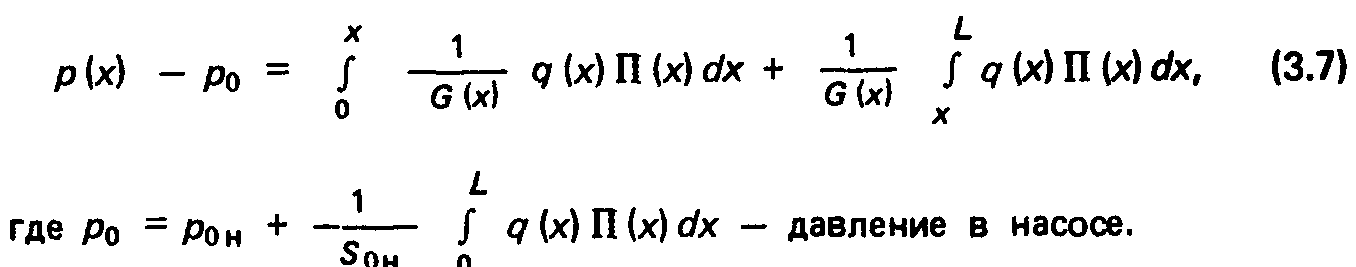
Ограничиваясь в этом параграфе стационарным приближением, легко показать, что абсолютное давление в х-м сечении стенками формируют диффузный молекулярный поток, поэтому молекулярная концентрация по тракту пучка складывается из двух компонент: пролетной концентрации молекулярного пучка и концентрации диффузного молекулярного потока. Последний составляет для средств откачки распределенную газовую нагрузку.

В масштабе энергий ионов молекулы, принадлежащие к диффузному и направленному потокам, неразличимы. В связи с этим соответствующие концентрации можно суммировать. Найдем эти концентрации и некоторые производные от них величины.

Из геометрических соотношений пролетную концентрацию молекулярного пучка в точке R (рис. 3.2) для квазиточечного источника, эмит-тирующего в трехмерное полупространство стационарный поток молекул N, можно представить как

В области малых R источник нельзя считать точечным. В этом случае, рассматривая эмиттирующую поверхность как круг радиусом р₀ и площадью F и применяя (3.8) для элементарного участка dF, получаем:

Для расчета давления в х-м сечении воспользуемся соотношением (3.6). Плотность потока q (х) определяется из геометрических соображений.

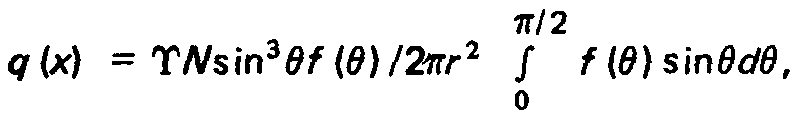
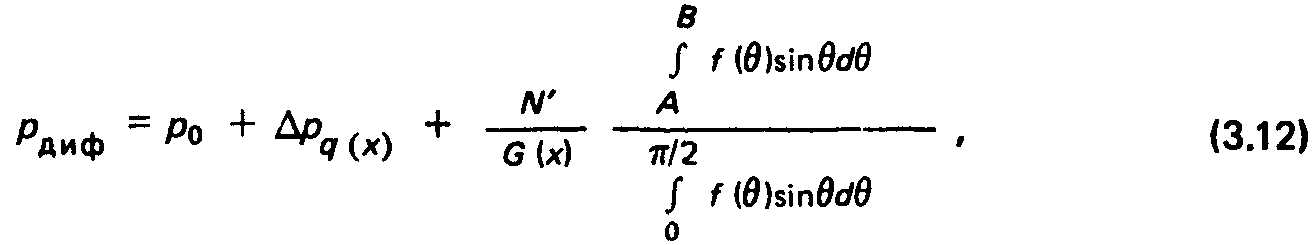
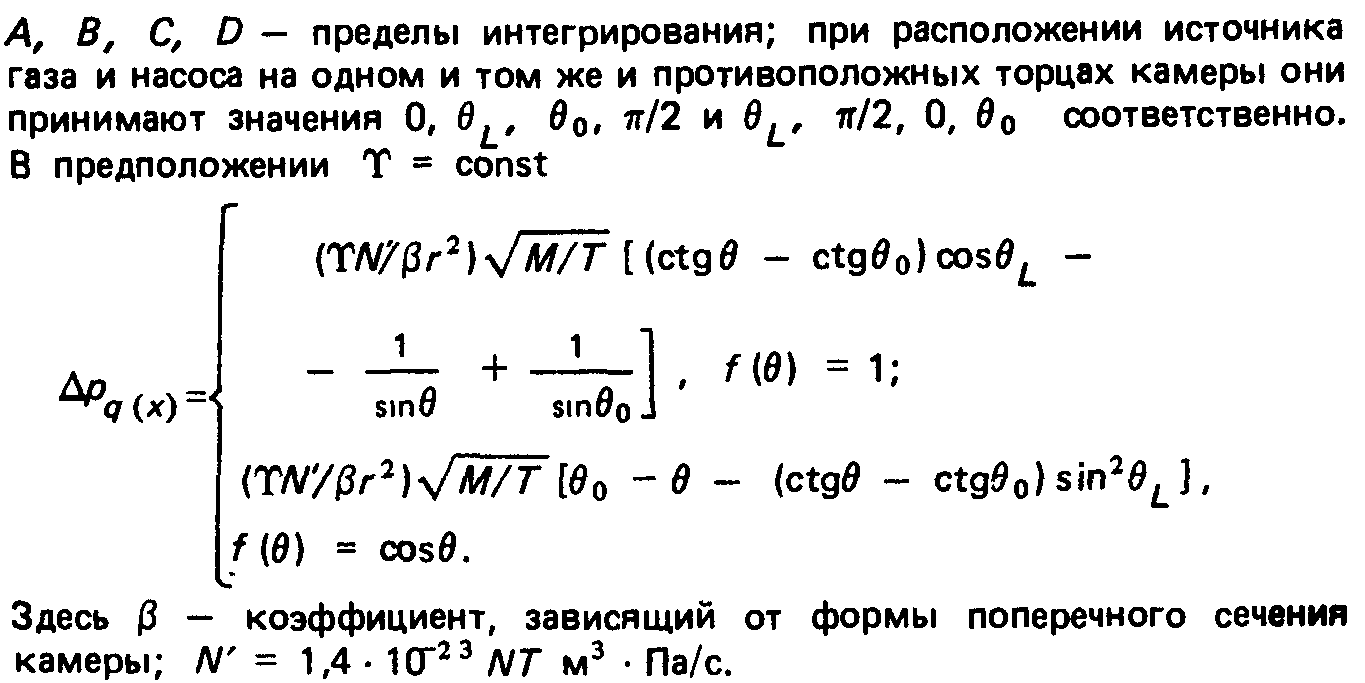
Найдем интегральную плотность молекул по тракту, определяющую интенсивность взаимодействия пучка с нейтральными частицами:

Приведенные соотношения иллюстрируются рис. 3.3 и 3.4: распределению f (i/) =1 соответствуют сплошные, a f (д) = cosi/ — пунктирные линии.

Рассмотрение однородных линейных систем завершим анализом распространения возмущений молекулярной концентрации в протяженной камере. Кинетика таких процессов, имеющих принципиальное значение при проектировании систем автоматизированного управления вакуумным трактом, описывается уравнением диффузии

Для равномерно излучающего эмиттера кругового сечения:

Для системы с совмещенными источником и насосом:

Для системы с источником и насосом на противоположных концах:

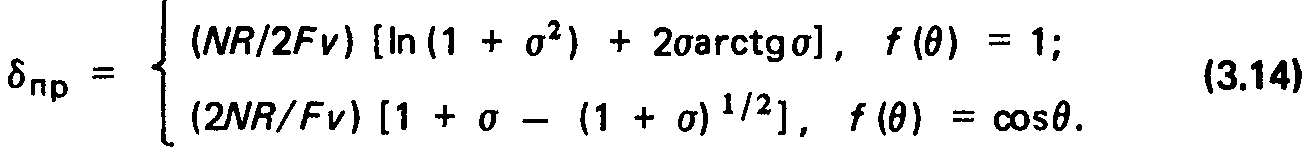
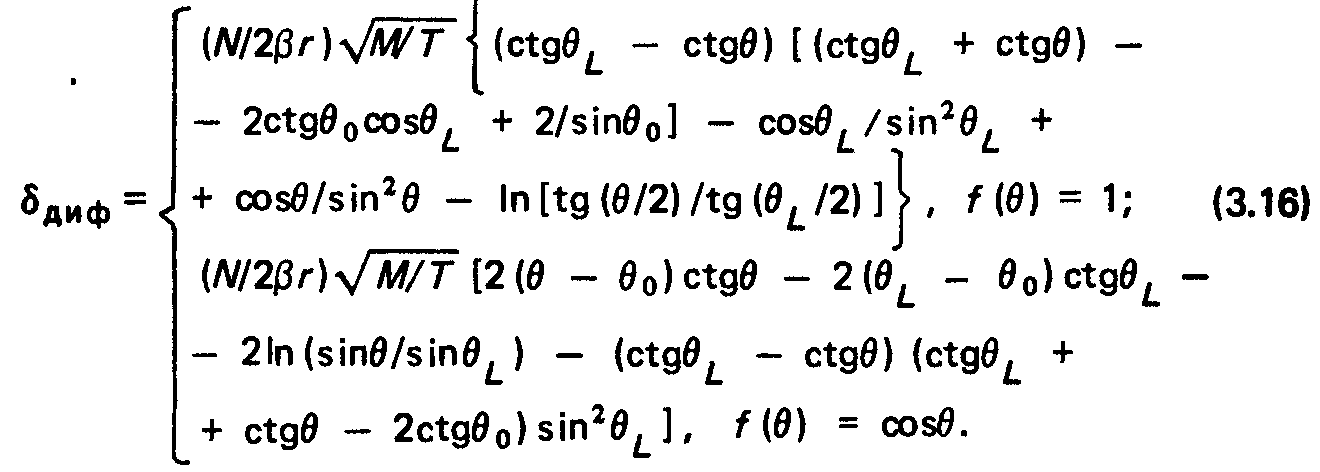
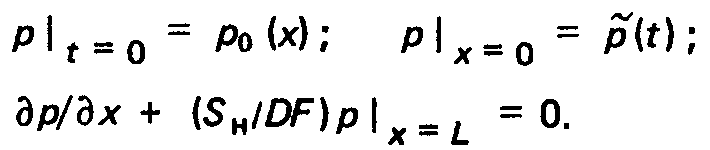
Решая уравнение (3.17) методом Пуассона, можно получить:

Формула (3.18) описывает распространение возмущений в протяженнои камере произвольных размеров при постоянной температуре. Начальное распределение р₀ (х) при t = 0 дается формулой (3.6). На рис. 3.5 представлены графики (р/р₀) (т) для различных сечений к при произвольно выбранном значении г = 10. Из (3.18) легко определить время с начала напуска газа, за которое давление в сечении к повысится на величину 5. В частности, когда натекание постоянно (а(т) = а), можно получить, ограничиваясь только первым членом ряда (д =Д1):

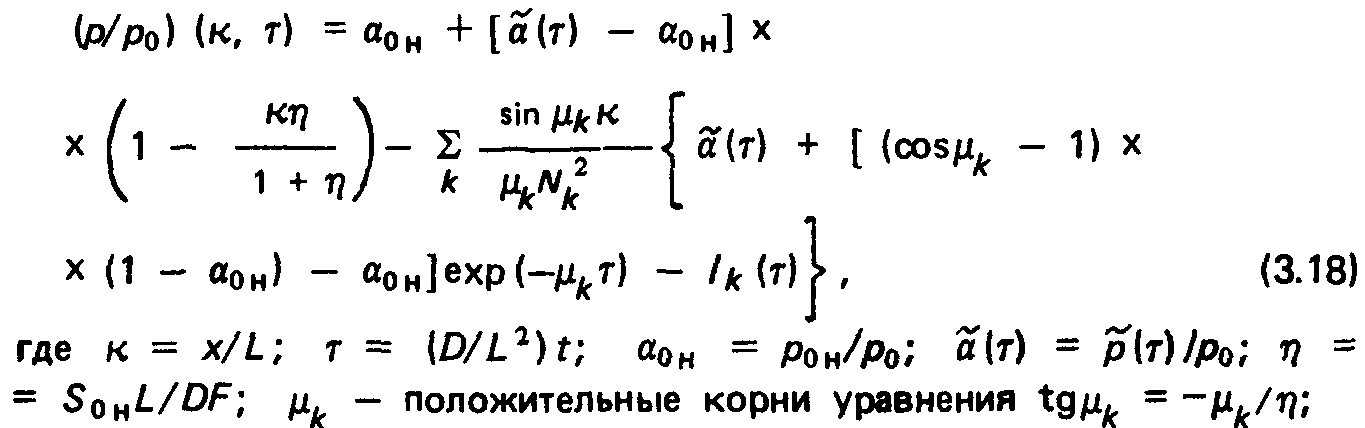
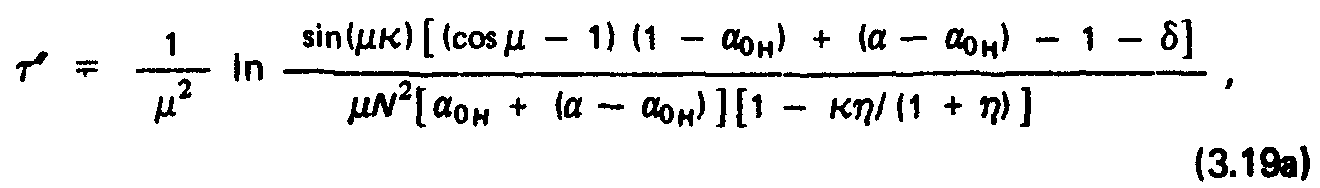
Приведенные зависимости в совокупности с соотношениями для газокинетической проводимости ускорительных трубок, диафрагмированных волноводов и других специализированных элементов ЭФУ {см. 3.3) и количественными критериями требуемого вакуума составляют математические модели ВС высоковольтных ускорителей, линейных ускорителей электронов, высокочастотных сепараторов, ионо- и электро-нопроводов и ряда других ЭФУ.

Приведем прежде всего параметры каналов и трубопроводов сравнительно простой геометрии, которые часто используются для формирования вакуумного тракта ЭФУ (рис. 3.6 и 3.7). Молекулярный поток падает на левый торец; справа от выходного отверстия находится свободное пространство. В левой части каждого рисунка показаны индикатрисы потока, формируемого в результате обратного рассеяния молекул; в правой части — индикатрисы потока вылетающих молекул. Индикатрисы построены в координатах к (б), в, где к (б) = АГ (в) /No; N_o — поток падающих на вход молекул в единичном телесном угле, ориентированном по оси; N(б) — поток молекул в единичном телесном угле в направлении в по отношению к оси.

Обращают на себя внимание следующие моменты. Во-первых, кривые пространственного распределения выходящего потока оптически прозрачных структур деформированы значительно сильнее, чем индикатрисы молекулярных потоков, рассеиваемых в обратном направлении.