Методы анализа молекулярного переноса — метод Монте-Карло
Метод Монте-Карло (ММК), называемый также методом статистических испытаний, является численным методом решения математических и физических задач путем моделирования характерной случайной величины. Движение отдельных молекул газа подчинено законам статистической физики и носит случайный характер. Поэтому ММК, состоящий в моделировании их движения, адекватен физической природе молекулярного переноса и может рассматриваться как универсальный метод вакуумно-технических расчетов.
Как пример рассмотрим алгоритм вычисления коэффициента Р для структуры из т поверхностей с одним входом и одним выходом. Этот алгоритм предусматривает операции, указанные на рис. 4.1.



БЗ — выбор направления полета молекулы. Траектория влетевшей молекулы задается параметрически:

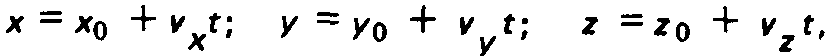

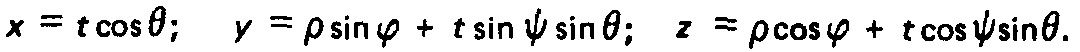
Для определения углов иОЙ справедливы следующие формулы. Поток молекул, попавших в элементарный телесный угол:

Плотность распраделения потока по углу:
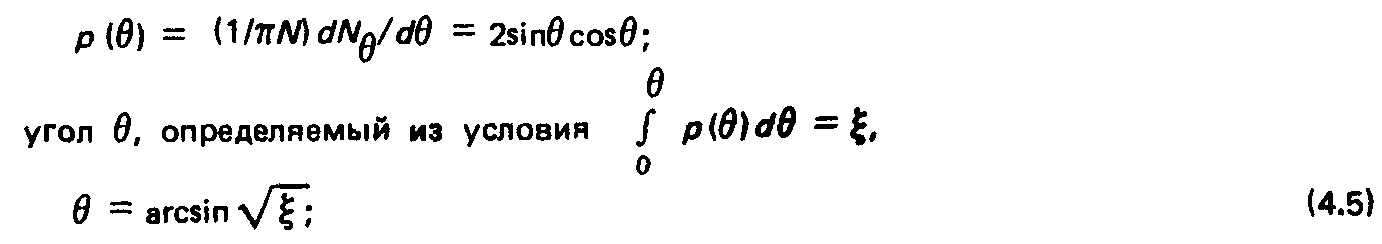

Случайные числа £ и х равномерно распределены на отрезке.
Для этого решаются N систем уравнений вида, располагая решения этих систем в порядке возрастания tj, так как каждой поверхности может соответствовать несколько корней) и выбирая среди них наименьший положительный корень t* = t. , искомые координаты полу-
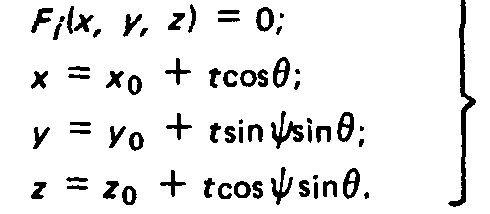
Погрешность вычисления значения а характеризуется дисперсией.
Можно показать, что где А — зависит от степени достоверности утверждения (4.9) и составляет 1 (достоверность 0,68), 2 (0,95), 3 (0,9975) и т. д. Обычно выбирают А =3, так что с вероятностью 0,9975 погрешность вычисления
Рассматриваемые в дальнейшем методы определения молекулярных и интегральных характеристик элементов ВС основаны на интегральных уравнениях тепло- и массолереноса. Аналитическое решение таких уравнений, кек известно, возможно только в простых структурех — параллельных плоскостях, концентрических сфе-рах, коаксиальных цилиндрах и т. п. В более сложных структурах приходится прибегать к численному интегрированию или зональному методу решения. Именно на этом принципе базируется рассматриваемый ниже метод угловых коэффициентов (МУК).
Основу зонального метода составляет замена непрерывного распределения искомых функций, входящих в подынтегральное выражение, дискретным. Поверхности, образующие ВС, разбивают на несколько зон, в пределах каждой из которых распределение исследуемой молекулярной характеристики принимается однородным. Число зон определяется требуемой точностью расчета; при повышении требований к точности это число необходимо увеличивать. Границы зон выбирают так, чтобы свести к минимуму различие между действительным ходом исследуемой функции и ее представлением в виде ступенчатой зависимости. Поэтому площади зон могут быть существенно различны: в области быстрого изменения исследуемой функции они должны быть достаточно малы. Эти области находятся обычно в местах скачкообразного изменения геометрической структуры — сужениях, расширениях, поворотах, а также в окрестностях локализованных источников молекулярных потоков. Если эвристический подход к выбору числа и границ зон затруднен, то на первом

Если выбранный корень соответствует мнимой, а не реальной поверхности, то берут значение Затем переходят на блок, соответствующий выбранной поверхности: ПО — фиксируются молекулы, вылетающие через входное отверстие; П1 — фиксируются молекулы, вылетающие через выходное отверстие; П1 — рассматривается взаимодействие молекулы с поверхностью F. *
Б5 — рассмотрение последующих действий. Если с помощью некоторых оценок выясняется, что требуемая точность еще не достигнута, то строится траектория новой молекулы (£2).
Б6 — вывод окончательных результатов. Коэффициент проводимости определяется соотношением (4.2). Коэффициент обратного рассеяния вычисляется с помощью числа молекул Л/вх, вылетающих из структуры через FBX:



Коэффициент захвата:



